 Weber
and contrast ratios
Weber
and contrast ratios Weber
and contrast ratios
Weber
and contrast ratiosThe ability of the visual system to discern intensities - the Weber fraction - is about 1%. Some people claim 2%. The exact number is open to debate, and subject to the choice of experimental conditions. Certain very demanding experiments can reveal an ability to discern intensity ratios of 0.5%, but those experiments do not reflect experience in image coding. What is loosely called the Weber fraction is known in color science as Contrast sensitivity.
Contrast ratio refers to the ratio of intensities between the most intense (brightest) and least intense (darkest) elements of a scene, an image, or a display. A CRT in an office environment rarely achieves a contrast ratio better than 10 to 1. A ratio of 30:1 is typical of viewing television in a living room. A very good cinema can achieve a contrast ratio of 100:1.
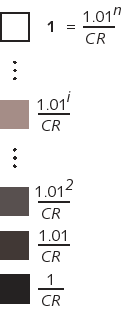
Consider this sketch of a set of discrete intensity levels, coded 0 through n. Maximum intensity white is at the top, with a normalized intensity of 1. The minimum intensity is defined by the contrast ratio, CR; its intensity is 1 divided by CR. (For a contrast ratio of 10, the minimum intensity is 0.10.
We assign intensities to intermediate code levels according to the Weber fraction. Code zero is the best achievable black. Code 1 has an intensity 1.01 times the minimum intensity, 1.01 divided by CR. Code 2 has an intensity 1.01 squared, divided by CR. We proceed up the scale, so that code i has intensity 1.01 to the power i, divided by CR.
To determine the number of steps, form the equation at the top of this sketch. The solution to this equation obtains the number of steps, as the logarithm of the contrast ratio divided by the logarithm of 1.01.
The table below shows the number of bits required for contrast ratios of 10:1, 30:1, and 100:1, for Weber ratios of 2%, 1%, and 0.5%. You can see that 7 bits is the bare minimum, with loose assumptions for the Weber fraction and a poor viewing environment. Ten bit coding is sufficient for a tight assumption about the Weber fraction, and demanding viewing conditions.
|
Contrast sensitivity | ||
| 2% | 1% | 0.5% | |
| Contrast ratio | |||
| 10 (office environment) |
116 (~7 bits) |
231 (~8 bits) |
462 (~9 bits) |
| 30 (living room, television) |
172 | 342 | 682 |
| 100 (cinema theater) |
232 (~8 bits) |
463 (~9 bits) |
923 (~10 bits) |
In video, we use power law coding and 8 bits; that achieves good performance at contrast ratios in the range of 30:1. (For high end video production, 10 bit systems are used.) In digital film work for the cinema, we use logarithmic coding, sometimes 8 bits per component, sometimes 10. In computer generated imagery (CGI) for the cinema, 12 bits is the minimum for linear light coding. In offset printing, practical dot gain - in the range of 20% - has the fortuitous effect of introducing a transfer function roughly comparable to the transfer function of a CRT, but with an exponent of about 1.8. Coding "dot percentage in film" in 8 bits, targeting a dot gain of 20%, achieves good performance in contrast ratios up to about 40:1 (corresponding to a DMAX of about 1.6)..
In his argument for linear coding, Timo fails to consider Weber's Law.
See also: Gamma FAQ - Linear and nonlinear coding
Charles Poynton
Copyright © 1998-07-27